In any language, the meaning of the words is determined by semantics; its logic, however, is embedded in its syntax. Therefore, "the same language" involves using identical semantics and identical syntax.
Many languages are spoken throughout the Western world. However, understanding among people is possible because all of these languages are based on the same semantic and syntactic categories; one language may differ from another in terms of : linguistic structure; however, all of them are isomorphic. This semantic and syntactic isomorphism makes possible translation, i.e., to reproduce in a given language the image of what has been said in a different one. Thus, the goal of "a common language" is achieved.
These remarks also apply to the relationship between computers and human beings. Let 's consider, for example, a computer program involving the following instructions: read the client's file; identify those who have not paid; send a type-A notice if payment is less than a month overdue; in other cases, send a type-B notice; however, if the client belongs to category 1, do not send any collection notice." These instructions can be written in different computer languages, provided their syntax can handle the logical schema involved in the instructions.
For the computer to execute this program, the circuits in the computer's central memory must be designed to handle the logical functions involved in the syntax of that particular programming language. Without these electronic circuits, the computer would not be able to handle such a program, and so its intelligence module would have to be expanded, or simply replaced.
However, if the logical capacity of the computer is underutilized because the syntax used by the programmer is inadequate, it would be advisable to replace that engineer with another who knows a more advanced language, which can give lnstructions adequate to the intelligence level of the equipment.
There is a centuries-old misunderstanding between the different social groups who live in the territories where the Qoya cultute flourished, especially in regions of present-day Peru and Bolivia. This misunderstanding predates the Spanish conquest, and still exists today because people do not speak the same language nor use the same system of logic.
If this really is the cause of the misunderstanding, one may well ask whose "logical circuits" must be reprogrammed so that all members of our society can fully understand each other.
My research on Aymara logic would appear to suggest some guidelines which could contribute to solving this centuries-old misunderstanding within our society, in which two essentially different systems of logic function at loggerheads.
Applying methods of mathematical logic, I have attempt to determine whether Spanish and Aymara-speaking people make inferences in different ways, and, if so, to identify the differences, the areas of misunderstanding, and the maximum logical understanding that can be achieved.
The idea that there is something special about Aymara which sets it apart from other languages is not new. Both the early scholars and modern linguists who have studied the Qoya language have been fascinated by its highly logical structure. Although they have not, of course, used the powerful methods of mathematics to test their ideas, they have provided very interesting and revealing analyses of key aspects essential to understand the syntax of this language.
These linguistic works are invaluable material which can serve as a starting point for multidisciplinary research, Computer science may contribute not only to an understanding of the language, but also to revitalizing this millenary culture and adapting it to today's modern world.
To achieve this ambitious goal, Aymara-speaking people must have access to world literature. This requires findin. a solution to all the technical problems involved in translating into Aymara. This brings us to the key issues: the problems of misunderstanding, and the psychological effects subsequent to the communication.
a) Level: determined by the language and system of logic of the sender, the translator, and the receiver;
b) Channel: determined by communication factors related to the environment, semantics, logic, ideology, and psychology, which influence communication as a whole. (1)
The following symbols are used as a key for the indexed file in which the different cases are stored:
/EAT/IAPT/RCB/5 (L, P)
In this example of misunderstanding, a message sent by an Aymara-speaking person, who thinks according to a trivalent system of logic, was translated into colloquial Spanish by another Aymara-speaking person who also thinks according to a, trivalent system of logic, for someone who speaks correct Spanish and thinks according to a bivalent sytem of logic; this is an example of case 5 within that category, and involves logical and psychological problems.
Some typical cases of misunderstanding related to the logical channels in particular are briefly discussed below. Collection, analysis, and classifìcation of cases are on-going activities, but proceed vesy slowly because of a lack of institutional support.
| ME: | 'kunalaykus ukjamaw luraraptapa?' For what (logical) reason is ít so (that way) that you have done it?/ |
| MI: | "Why have you so done it to him?' (no distinction regarding the kind of "why?") |
| MT: | "Why have you done it to him?" (He does not feel "so", "this way" is necessary) |
| MR: | "Why (for what reason) have you done it to him?" (giving a causal interpretation to "why?") |
Faced with a question so distorted by the interpreter, the receiver will give an answer which implies cause or motive, for instance:
"Because I wanted to help him."
However, the sender was expecting an explanation about the manner of doing it, for example "Because a use in this way we save time, since ..."
In this case, the misunderstanding is due to the fact that Spanish does not have different words to translate the various "why's?" of Aymara:
'kunalaykus?'
(a reason or logical cause is asked.for)
'kunasupas?'
(asking about the cause in the sense of a cause and effect relationship)
'kuna çuymampirakis?'
(the motive or psychological cause is demanded)
Although the difficulty has an impact on the logical and psychological channels, its origin lies in the semantic channel because of the vague meaning of the Spanish "por qué? /why?/; however, if we search even deeper, we may find that the true cause of this case of misunderstanding lies in the ideological channel.
Bertonio wrote his grammar between 1585 and 1602. Apparently, at that time he was not yet pressured by church authorities, as he may have been when he published his dictionary ten years later. The roles of the suffixes "layku" and "supa" are clearly explained in his grammar (p. 210). The word "layku" meaning "reason" can still be found in his dictionary, although the word "supa" is already tainted by ideological connotations (the theology of those times), to such an extent that "supayo" is translated as "devil" (LB1- 328).
The explanation is more or less obvious: the word "supa" when used as a nucleus, not as a suffix, means "cause"; therefore, the verb "supaña" should mean "to cause", and the verb "supayaña" would mean "to make to cause". Thus, "supayo" would mean something like "the one who causes", or "cause of causes". Every word fundamental to Qoya ideology was combatted by the Church, which managed to associate them with demoniacal concepts. Another typical example is the word "yatiri" ("wise man"), derived from the verb "yatiña" (to know), which is sometimes, even today, translated as "sorcerer".
There is another kind of difficulty related to the Spanish word "por qué?", and especially the English word "why": The answer is introduced by "porque" /because/, This is not the cas in Aymara: the same suffix "layku" is added at the end of the answer; for example "ukalaykü" (because of that). However, the missionaries, most of whom are English-speaking, have coined the term "kunalaykutej" to translate the English word "because", trying to impose English syntax on Aymara. This, of course, causes serious misunderstandings in the psychological, logical, and semantic channels, but which originate in the ideological channel.
ME: 'mañana he de estar viniendo nomás' /I will be coming tomorrow
probably/ (the speaker indicates his desire to come, but does not commit
himself) 'çaruru jutaskatki' (thinking in Aymara)
x.'ska.ki = (1,1,1)
Trivalent tautology, always true, never a lie.
MR: "mañana vendré" /I will come tomorrow/ (neglecting the modalities expressed in Aymara)
Result: A poor logical translation causes psychological conflict; if the sender does not come tomorrow, the receiver will consider him a liar, although he has told no lie because what he has said is a tautology, and he is always right. This kind of sentence using the gerund, and the word "nomás" /probably/ at the end is very frequent in the variety of Spanish spoken in La Paz, especially in the case of "promises" which are never kept. Speaking of tautologies, it should be brought to the attention of those readers well versed in logic that the statement "x or not x" is a tautology in bivalent logic, but not in a trivalent system because its kimsaku is:
x\/N(x) = (1,0,1) (quasi-tautology)
instead of : (1,1,1) (tautology)
as can be seen from Lukasiewicz's truth-tables.
In trivalent Aymara logic, besides the normal alternative "\/", there is the stochastic alternative "\./"; it is evident that "x\./N(x)" is a tautology, as can easily be shown with the pä-kimsaku for the statement:
x\./y = x.sal.la + y.salla + xy.sti = (1,0,1,1,1,0,1,0,-1)
where y = -x. In column 5, where x = y = 0, the value is 1, and not 0 as in the case of normal altarnative.
ME: x.ti = 'wawaruj manqaytati?, (the suffix ti has been chosen by
mistake, following the recommendations in some grammars)
"did you feed the wawa?" (this is what he wanted to ask)
MR: "By any chance have you fed the wawa?" (correctly interpreting the meaning of ti)
Result: The modal suffix ti is misused and the interrogative statement is formulated in the logical channel in the negative form. The question should have bean "wawaruj manqaytasti?" ('and have you made the wawa eat then?')
In the psychological channel the receiver is offended by the sender's insinuation of doubt concerning his having fed the wawa, when in fact the sender merely expected a confirmation that she had in fact been fed.
It should be pointed out that: x.ti = (-1,1,0)
whereas x.sti = (1,1,-1).
The question could also ,have been posed using the antonym form of x.ti:
x.ça.ti = 'janiça wawaruj manaqytati ?' (or have you not fed the wawa by any chance?), the kimsaku of which is (0,1,-1)
ME: The sender, because of ideological reasons in the channel of the means of communication, tries to use the orthographic rules of Spanish to transcribe Aymara; thus, the suffix "ka" is sometimes written 'ca', and sometimes 'qui'.
MR: The phonetic inconsistencies of Spanish are foreign to Aymara, a consistently logical language; thus, the receiver interprets 'ca' and 'qui' as two different suffixes, and possibly interprets "qui" as "ki", which may lead to a great deal of misunderstanding.
For example:
x.ka.ti = 'jumaj janiw jutktati.' (you have not come)
'jumajj janiw jutctati.' (Hispanicized orthography)
x.ka.ti = 'jupaj janiw jutkiti (He (or she) has not come)
'jupajj janiw jutkiti.' (Hispanicized orthography)
Explanation: The present perfect tense requires the suffix "/" which causes the elision of the "a" in suffix "ka". The suffix "ta" is the equivalent of the pronoun "you"/sing./ but "i" is the equivalent of the pronoun "he". In Spanish "ci" is not pronounced like "ki"; therefore, the same suffix "ca" must be written "qui". This inconsistency is not a problem for Spanish-thinking people, who do not have to be constantly identifying suffix strings when reading, as is the case for Aymara. However, this is a serious obstacle to both Aymara-thinking people and computers used for translation into Aymara; it is also unnecessary, since there is no reason to impose Spanish orthographic rules on the Aymara language.
| ME: | 'qaruruj jutam!' (misuse of the imperative, due to
lack of education)
'tomorrow (to the party) you must (certainly) come.' (.what speaker intended to say) |
MR: 'Come tomorrow!' (imperative form of command)
Results: The incorrect utilization of modal suffixes in the channel generates feelings of offense in the psychological channel, because in Aymara the imperative is used only in rare circunstances, and is only acceptable when used by a person who has legitimate authority to exert command, for instance the mother of a minor.
The correct form would have been: 'qaruroj jamapini jutata!' (tomorrow you always must come for sure!)
Another negative question which must be used carefully is: x.ti.sti = (-1,1,1).
for example:
'luraraptatisti?' (and by any chance have you done it for me yet?)
This implies serious doubt about your having done it for me. It should be pointed out that this statement is the opposite of a statement conveying possibility, i.e., in formal logical language it means: "it is possible that you have not done it for me.
Below is an interpretation in popular Spanish of two frequent antonymous expressions that must not be confused:
| x.sti = | 'jiçasti?' (1,1,-1) 'And now then (what do we do)?' |
| x.ti.sti = | 'jiçatisti?' (-1,1,1) 'And by any chance now then (has that happened)?' |
The part implied in the expression appears between parentheses.
| ME: | 'aka warmej jarisa payisa.' (connective
wothout connective term). "This woman either washes /clothes/or cooks" (what speaker intended to say) (JJE-197). Because the sender has omitted the connective "uka.A" , the receiver is forced to assume any of at least three possibilities: |
| MRl: | 'aka warmej jarisa payisa ukkasa.' 'La mujer èsta ya sea que lava o cocina "This woman either washes or cooks (perhap both, but one for certain)." |
| MR2: | 'aka warmej jarisa payisa ukaspi.' 'La mujer ésta ni lava ni cocina ni siquiera pues.' 'This woman neither washes nor cooks for sure' |
| MR3: | 'aka warmej jarisa payisa janit ukjamaça?' 'La mujer ésta acaso no lava ni cocina entonces?' 'This woman by any chance does not wash or cook then?' The stochastic alternative is also equivalent (in the bivalent part): 'aka warmej jarisalla payisalla ukasti.' |
Using the operational method explained in the last chapter, it is easy to see that the Spanish interpretations of the above-mentioned statements are in accordance with their respective truth-tables:
| x= | 1 | 0 | 1 | 1 | 0 | -1 | 1 | 0 | -1 |
| y= | 1 | 1 | 1 | 0 | 0 | 0 | -1 | -1 | -1 |
| x.sa+y.sa+xy.ka.sa = | 0 | 1 | 1 | 1 | 1 | -1 | 1 | -1 | -1 |
| x.sa+y.sa+xy.sa.pi= | -1 | -1 | -1 | -1 | -1 | 0 | -1 | 0 | 1 |
| x.sa+y.sa+xy.ti ça = | 1 | -1 | -1 | -1 | -1 | 0 | -1 | 0 | 0 |
To verify the calculations the reader must keep in mind that
xy.A is (xy).A.
The fact that the same logical suffix can be used to generate various kinds of connective statements has always baffled linguists, who have a bivalent bias and prefer clear, "unambiguous" functors. For example, in his grammar, M. Hartmann goes so far as to say therte are no functors in Aymara: In his grammar, Tarifa uses the adversative conjunction "neither" to transate the logical suffix "sa", whereas Ebbing prefers the alternative conjunction "or", and Middendorf, "and."
To be able to use an adequate logical model which will lead to the desired conclusion, following a given inferential schema, the problem must be phrased as an inference, i.e., a system of equations with the propositional variables which represent the statements forming the given premises and the conclusions we want to reach. In everyday life, most inferential problems involve giving and receiving instructions which can be expressed in simple terms and handled by the syntax of the language. These inferences are so common that their mere enunciation leads us almost automatically to the conclusion.
For instance, if a contract stipulates that "if A works, then B will pay him", it stands to reason that if this does not happen, it is because A has worked, but B has not paid him. Some people may be "more logical" than others and able to handle more complex problems involving several statements: in any event, the valid formulation of logical problems depends on the correct use of connective words according to the syntactic rules of the language.
When we enter the realm of modal logic, where statements canot be worded with total precision using everyday language, one must resort to symbolic logic, and use formulate to phrase inferential problems. However, as seen in previous chapters, Aymara syntax makes it possible, using logical suffixes, to understand a great many modal statements in an unequivocal manner. Now; to determine the degree to which an "Aymara-thinking person" can infer conclusions, without resorting to mathematical symbols, is outside the scope of our research on Aymara logic. It is evident that this language has tremendous possibilities because modal statements can be consistently expressed in very compact form. This makes it possible to retain in memory numerous inferential schemata which sometimes cannot even be expressed in other languages.
It is also true that in Spanish people do not always use all the available possibilities to phrase statements precisely, and to infer conclusions "mentally", that is to say, without recourse to pen and paper. For instance a survey among educated people would show that a large percentage of them do not know how to clearly differentiate between the alternative "p or q" and the disjunctive "be it either p or q", even within the limited framework of bivalent logic. This lack of distinction between the connectives of language can even be seen in scientific documents where the neologism "and/or" has been introduced; there is only one truth-table that can be assigned to it: the one corresponding to the alternative conjunction "or".
It is not surprising therefore, that uneducated people are unable to avail themselves of all the possibilities offered by a language as logical and powerful as Aymara. Socio- linguistic research would help to determine to what extent Aymara-speaking people really make use of all the logical possibilities of their language.
The sentences in the examples which appear in previous chapters have almost all been taken from grammar books which record Aymara as it is actually spoken. These examples have been very useful to show the logical structure embedded in the syntax of this language, the mathematical properties of which have been presented. Hereafter, we are on our own. It is not my intention to invent examples in Aymara to study three-valued logic; however, I will try to generate statements which express inferences, always strictly respecting the gramatical rules of Aymara and applying the results of my research on the functions of logical suffixes.
Readers who learned Aymara in childhood can check the validity of these formulations, and determine whether they allow them to "mentally infer" mathematically demonstrable conclusions. These formulations have been translated as accurately as possible and are provided to enable all other readers to appreciate the approximate meaning of those statements; in all instances the corresponding truth-values and algebraic calculations which prove the validity of our resuits are given.
Since our goal is to investigate the potential value of Aymara logic for inferential analysis, our efforts will be directed mainly at problems which cannot be solved by using Aristotelian logic. Specificaliy, we wish to show the advantages of Aymara logic for solving inferential problems involving uncertain premises, while emphasizing the practical value of this approach. For example, let us analyze a classical problem of inference as seen from the perspective of an Aymara.
Once upon a time, Aristotle, the founder of Greek logic, disciple of Plato, member of the court of Philip of Macedonia, tutor to Alexander the Great, went for a walk in one of the beautiful spacious gardens of Olympus. His curiosity was suddenly aroused by an Indian woman, possibly named çoqewanqa, a native of Taypi Qala. She was sitting on the ground thinking, her attention concentrated on a row of kuka (coca) leaves which were laid out in front of her. They engaged in the following conversation:
Aristotle: Say, my good woman, why are you so absorbed with those leaves?
Çoqewanqa: Ah! Hiya, pop, how do you like my game?
Aristotle: Game? Come now! Tell me what sort of game you are playing on the ground.
Çoqew: This is a logical matrix, pues/for sure/; it helps me infer from these premises the value of that conclusion (she points to the rows)
Aristotle: Are you telling me you cannot think logically, and therefore you must resort to such a primitive aid to make simple inferences?
Çoqew: Hey, mister, do you think this is a simple inference? Can't you see there are so many compound premises I can't remember all of them at the same time? My leaves help me to calculate the result without having to wrack my brains. Now, tell me, mister, could you do it without help?
Aristotle: Are you trying to solve a syllogism?
Çoqew: Syllogism? What's that? Explain what ya mean!
Aristotle: Well, I think that before we get down to business we must check whether you and I can converse on logical matters. I will pose a simple problem of inference; if you can solve it, we can proceed. If you can't,'its of no use trying.
Çoqew: OK man, let's go.
Aristotle: Can you see the two gentlemen chatting by that tree? Well, one is Plato and the other is Socrates, two great philosophers who, as you surely know, made enormous contributions to mankind.
Çoqew: I dunno that.
Aristotle: Well, now you know. All right now. Socrates once told Plato: "I won't want to visit you unless you want to visit me." Plato replied saying: "I won't want to visit you if you want to visit me, but I will want to visit you if you do not want to visit me.' Now, tell me, what did Socrates and Plato want?
Çoqew: That's really simple, you know. No wonder you don't use coca leaves for that. The Socrates doesn't want to visit the Plato ... On the other hand, the Plato wants to sisit the Socrates nomás /probably/
Aristotle: Well done, cunning Indian! I see you can think straight. Let's go on.
Çoqew: Wait a second mister! Now it's my turn to pose a logical problem to make you think.
Aristotle: I see you don't know how to show respect, but all right, I'll listen to you.
Çoqewa: The
problem is almost identical to the one you gave me, the only difference is:
'Socratej janit Platunaru tumpasiniña munkitiça Platonej
Socratesaru tumpasiniña munaspallaça tullanska'.
Aristotle: What the hell is that? What language are you.speaking?
Çoqew: Hey man, you are really ignorant! Didn't you know that we Qoyas already spoke Aymara long before you were born? What I said to you is that, in this case, the first premise is: "be the Socrates perhaps will not want to go visit Plato, or be the Plato will not really want to visit the Socrates, but."
Aristotle: (after thinking for quite a while). If I have understood you correctly, what you are trying to tell me is that now the premise is: "It is questionable that Socrates wants to visit Plato, although it is possible the latter still wants to visit Socrates". Right?
Çoqew: That's good. You have said it beautifully, more or less, but. Now go on with that inference of yours.
Aristotle: Although you have been able to phrase a premise involving modal statements and, I must admit, you have formulated a hitherto unstudied modality, viz, the probability modality, you seem unaware that one cannot arrive at a conclusion this way. How can one arrive at something certain from something which is only probable?
Çoqew: Not long ago, a young man by the name of Jan Lukasiewicz arrived in Olympus. He uses formulate to arrive at conclusions from modal premises. Perhaps he can help you, maybe.
Aristotle: I am aware of the papers on three-valued logic published by that Pole, but his mathematical notation is not widely accepted. Don't tell me you know it already!
Çoqew: I only know how to infer using my coca leaves, which I place in order according to the suffixes used in Aymara to set out premises and conclusions. I can teach you if you want, but.
Aristotle: OK. Let's see what can be done by those Qoya people you are so proud of. Show me how one can infer the conclusion of the problem you posed.
Çoqew: It's really eazy! My result is just the opposite of the former one, see! No doubt in this case the Socrates wants to visit the Plato, but the Plato doesn't want to visit the Socrates.
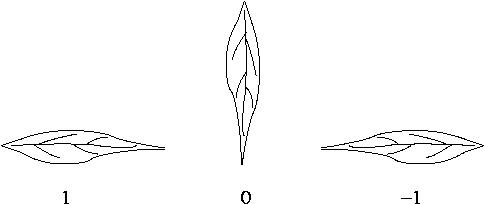
Aristotle of Stagira was perplexed by the unequivocal demonstration made by çoqewanqa, who used her coca leaves to display the truth-table shown below. When using coca leaves, the three truth-value are represented by these three positions of the leaf:

Each row of leaves is a pakimsaku for each proposition made up of two simple statements which, in our case, are:
The modalities used by çoqewanqa can be expressed formally:
| p = x.ti.ka = | 'It is controversial that it is false that Socrates wants to go to visit Plato' |
| q = y.su.lla = | 'It is improbable that Plato possibly wants to go to visit Socrates.' |
Thus, the first premise is the alternative which can be written
"Be that it is p, unless it is q"
The following truth-tables correspond to both versions of the problem, Aristotle's and Çoqewanqa's:
| Aristotle's | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| x = | 1 | 0 | -1 | 1 | 0 | -1 | 1 | 0 | -1 |
| y = | 1 | 1 | 1 | 0 | 0 | 0 | -1 | -1 | -1 |
| P1:(-x)\/y= | 1 | 1 | 1 | 0 | 0 | 1 | -1 | 0 | 1 |
| P2: x=>(-y)= | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| P3:(-x)=>y= | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | -1 |
| Çoqewanqa's | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| p=x.ti.ka.ti= | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 |
| q=x.su.lla= | -1 | -1 | -1 | -1 | -1 | -1 | 0 | 0 | 0 |
| P1:p\/q= | 1 | -1 | 0 | 1 | -1 | 0 | 1 | 0 | 0 |
| P2:x=>(-y)= | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| P3:(-x)=>y= | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | -1 |
It should be pointed out that in both cases the premises of implication (P2 and P3) are identical and are not modal. However, premise P1 differs in the two versions, and in Çoqewanqa's version it is a modal premise. The conclusion appears in the column in which all premises are met. As can be seen, in Aristotle's version in the third column, x =1, y =1; whereas in Çoqewanqa's, it is in the seventh column, x = 1; y = -1.